Continua il percorso combinato tra numeri, frazioni e geometria.
Il lavoro è già iniziato nel post intitolato TANGRAM: CONGRUENZA, EQUIESTENSIONE E FRAZIONI
Il dibattito è partito disegnando nel tangram una griglia quadrettata per aiutare i bambini nella valutazione di ogni forma rispetto all’intero quadrato.
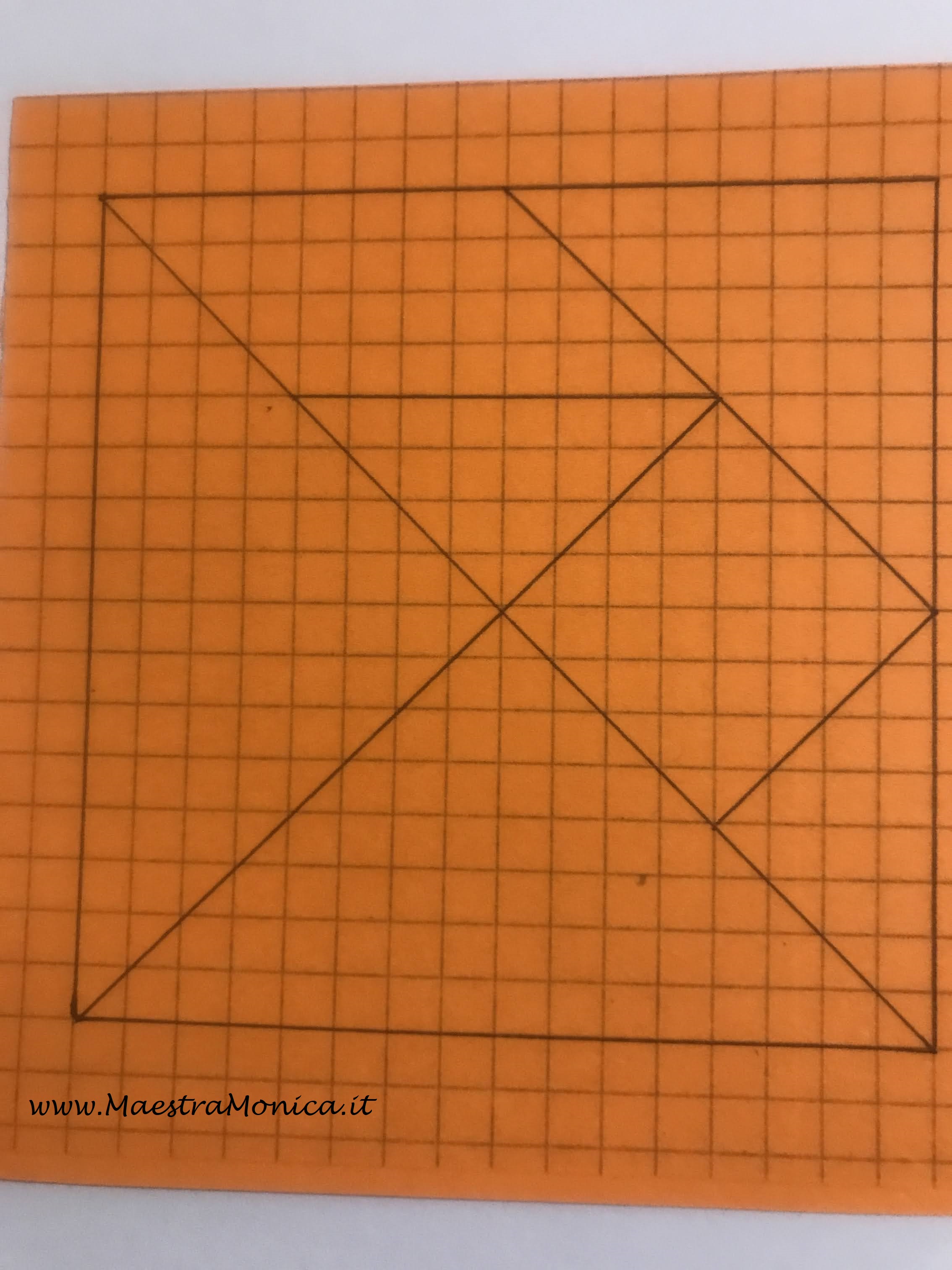
Il tangram è ulteriormente diviso in quadretti da un centimetro di lato.
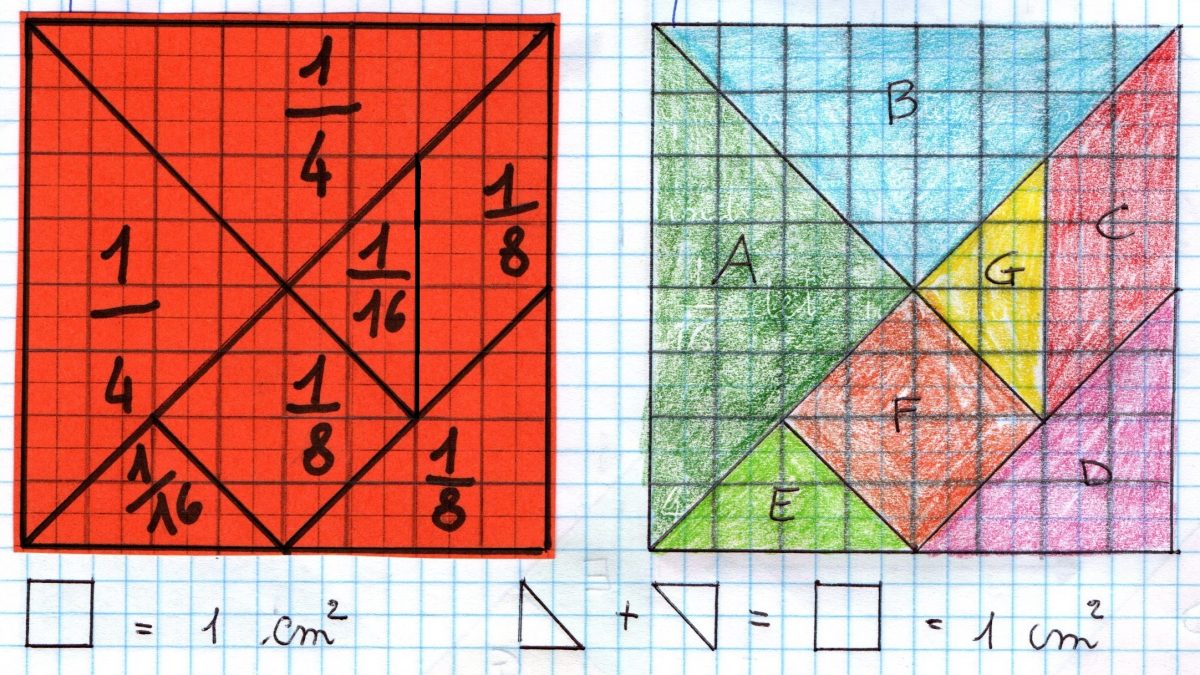
Riflettiamo: un quadretto vale 1 cm quadrato e due mezzi quadretti formano un centimetro quadrato.
Usiamo i centimetri quadrati come unità di misura per trovare le relazioni tra le aree dei vari pezzi del tangram. I singoli pezzi diventano unità di misura per contare quante volte il pezzo è contenuto nel tangram.
Esprimiamo le relazioni usando il linguaggio delle frazioni.
QUANTI PEZZI “A” O “B” SERVONO PER COMPLETARE IL TANGRAM?
Servono quattro triangoli grandi!!!
Allora il triangolo grande vale UN QUARTO di tutto il tangram.
CALCOLIAMO L’AREA DEI PEZZI E DI TUTTO IL TANGRAM.
Come possiamo procedere?
1° PROCEDIMENTO: contiamo i quadretti/centimetri quadrati.
AREA del tangram= 64 cm quadrati
AREA del triangolo grande= 16 centimetri quadrati
2° PROCEDIMENTO: il triangolo grande si ripete 4 volte nel tangram
AREA del tangram = 16 x 4 = 64 centimetri quadrati
Il triangolo “A” è un quarto del quadrato tangram
AREA A= 1/4 di 64 = (64:4) = 16 centimetri quadrati
3° PROCEDIMENTO: la misura di una dimensione si ripete tante volte quante la misura dell’altra dimensione, cioè uso la moltiplicazione.
AREA del tangram= 8 x 8= 64 cm quadrati
I bambini hanno continuato ad esprimere considerazioni e riflessioni analoghe anche in relazione agli altri “pezzi” del tangram.
Il percorso è riassunto sul quaderno.
LAVORO SUL QUADERNO



I bambini hanno notato che il valore di uno stesso pezzo può essere espresso con frazioni diverse e che il rapporto tra numeratore e divisore aumenta o diminuisce contemporaneamente moltiplicando o dividendo.
Tra i diversi pezzi esistono delle relazioni che possiamo esprimere con le frazioni.
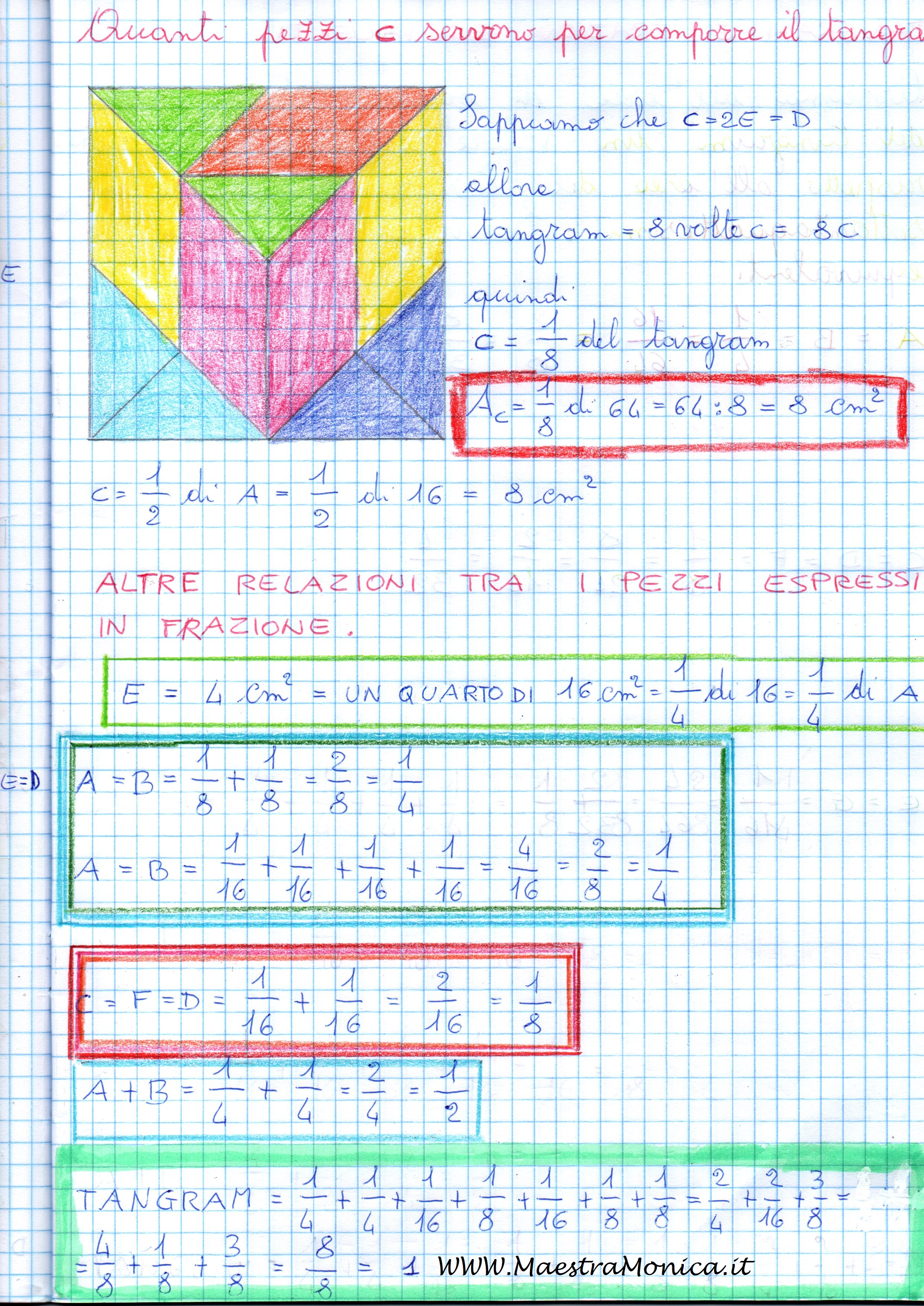
Il percorso si conclude ricercando frazioni equivalenti in riferimento all’area espressa in sessantaquattresimi.
LE FRAZIONI EQUIVALENTI SONO FRAZIONI CHE, PUR AVENDO NUMERATORE E DIVISORE DIVERSO ESPRIMONO LA STESSA PARTE DELL’INTERO.





