I bambini hanno sperimentato che per far compiere ad una figura una rotazione occorre fissare:
- UN PUNTO che individua il centro di rotazione;
- UN ANGOLO la cui ampiezza indica l’intensità della rotazione;
- IL VERSO orario o antiorario.
Ruotiamo una bandierina in senso orario.
I bambini osservano che la bandierina A per arrivare nella posizione B ruota di 90° cioè di un angolo retto…anche per ruotare da B a C , da C a D e da D ad A la bandierina ruota con un angolo di rotazione di 90° cioè ruota di un quarto di giro.
Se A ruota di 180° in quale posizione arriva?
In quale posizione arriva la bandierina A se ruota di tre angoli retti?…l’angolo di rotazione misura 270°.
Di quanto deve ruotare la bandierina A per arrivare nella posizione di partenza?
Nel quaderno verbalizziamo le rotazioni effettuate e le osservazioni che ne sono scaturite.

Ruotiamo la bandierina in senso antiorario con un angolo di rotazione di 45° cioè di mezzo angolo retto o di 1/8 di giro.
Per disegnare l’asta della bandierina nella nuova posizione in cui è ruotata i bambini utilizzano il goniometro misurando l’angolo di 45°.
Osserviamo i quadretti e rileviamo che l’asta della bandiera ruotata di 45° divide il quadretto del foglio a metà secondo la diagonale. Anche senza goniometro è possibile disegnare un angolo di 45°!

I Bambini riproducono su un foglio di carta trasparente la bandierina A , la fissano con la punta della matita nel centro di rotazione, poi ruotano il foglio trasparente ed infine riproducono la figura nella nuova posizione ruotata ogni volta di 45°
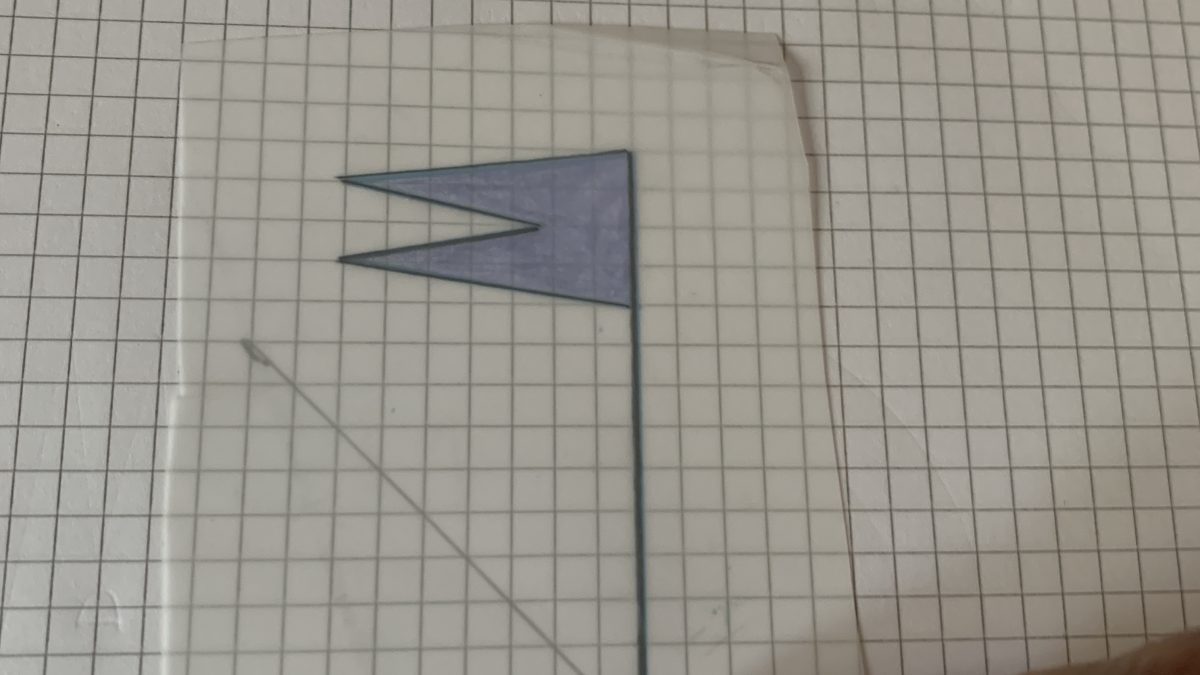

Continuiamo a riflettere sulle rotazioni della bandierina A.
Di quanto deve ruotare la bandierina A per arrivare nella posizione B?
Se A ruota di 90° in quale posizione arriva?
In quale posizione arriva, se la bandierina A ruota di 225° ?
Se A ruota di 3/8 di giro, in quale posizione arriva?
Verbalizziamo nel quaderno le rotazioni effettuate e le osservazioni che ne sono scaturite.
Con la rotazione si è parlato anche di angoli, ampiezza, frazioni, unità frazionaria (1/4 di giro, 1/8 di giro e 1/2 di giro) frazioni equivalenti che indicano la stessa ampiezza (2/4 di giro=1/2 di giro=4/8 di giro) e frazioni apparenti che rappresentano un numero intero (4/4=2/2=8/8=1 giro).
La rotazione, assieme alla simmetria e alla traslazione, è una ISOMETRIA che significa “UGUALE MISURA”.
Uno schema per fare sintesi delle caratteristiche delle isometrie.
