In classe, utilizzando spago e cannucce i bambini hanno costruito diversi poligoni, hanno provato a deformare i poligoni costruiti e hanno potuto constatare cosa significa che il triangolo è l’unico poligono indeformabile e che...il triangolo è il poligono con il minor numero di lati.
Pur con questa limitazione, i bambini osservano che esistono numerosi triangoli di diverso tipo: la loro classificazione può essere operata sia rispetto ai lati sia rispetto agli angoli – Il nome dei triangoli –
L’attività di scoperta delle caratteristiche dei triangoli continua costruendo un modello dinamico per i triangoli isosceli di Emma Castelnuovo con il quale si possono fare tantissime osservazioni riguardo la base, l’altezza, i lati, gli angoli e il punto medio.
La sua realizzazione è molto semplice: si usa un cartoncino come base, due ferma campioni, un elastico e un pezzo di spago.
E’ facile vedere che tirando lungo la linea perpendicolare che rappresenta l’altezza i triangoli sono tutti isosceli.
I bambini realizzano sul quaderno quanto osservato.
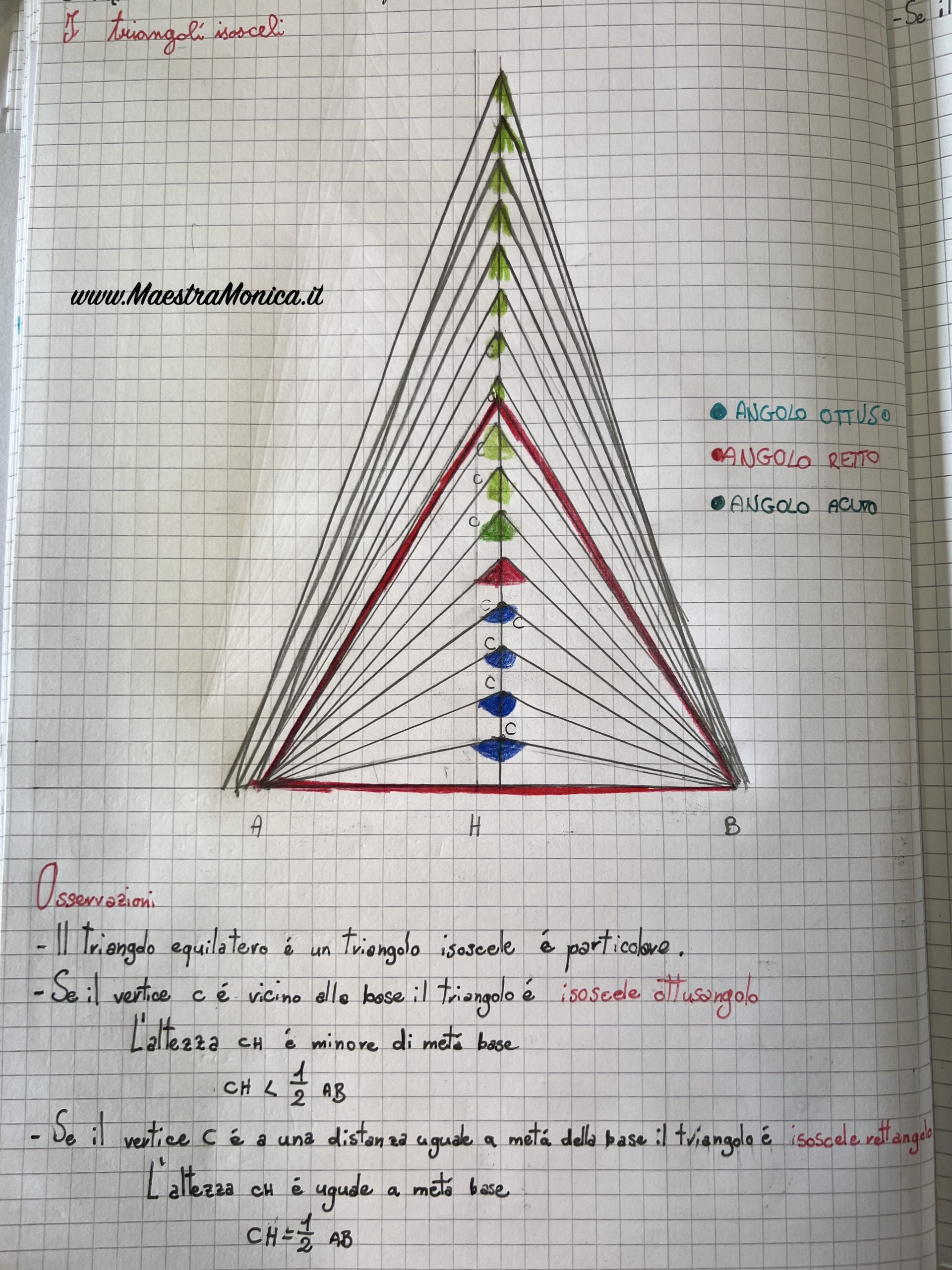
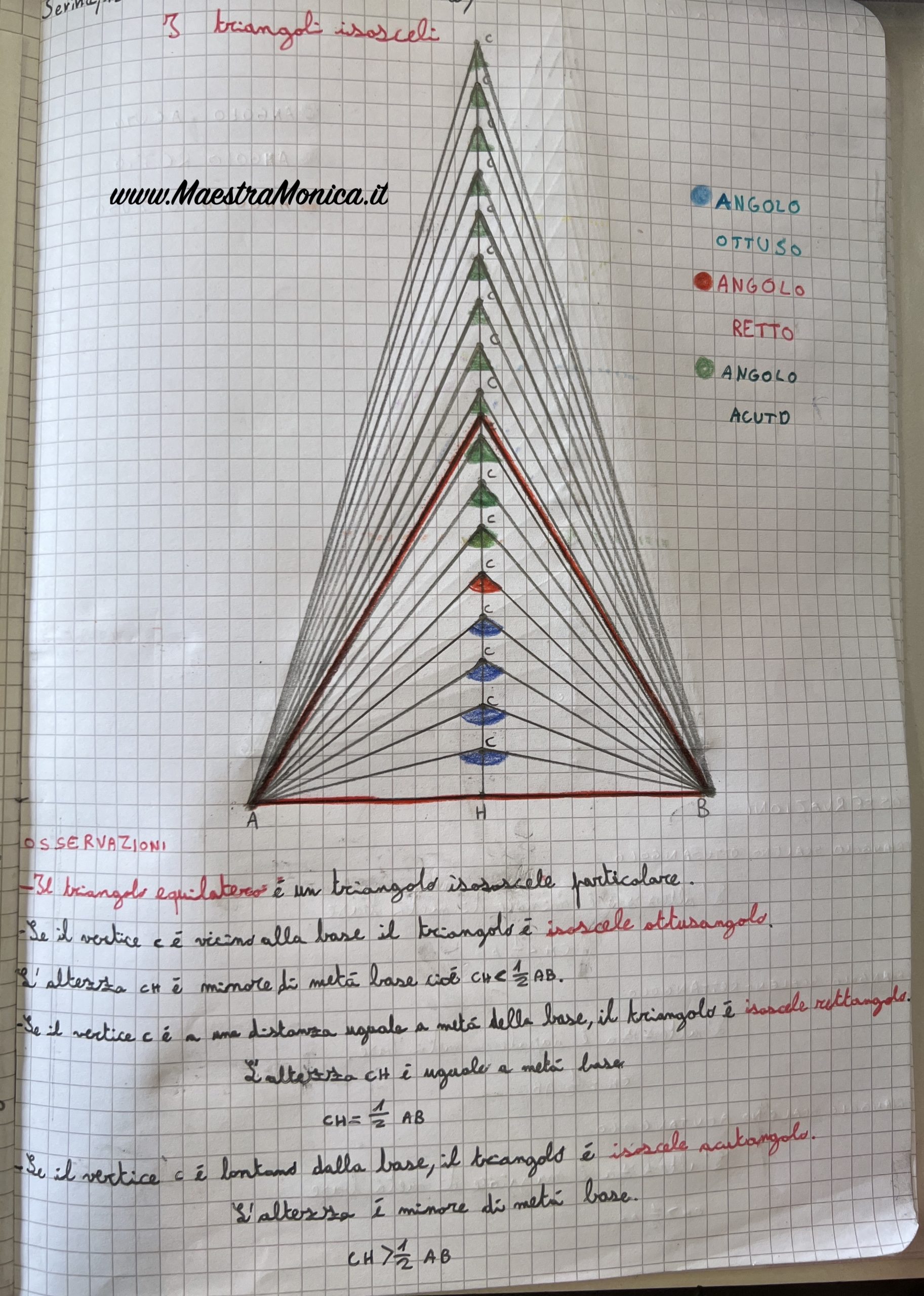
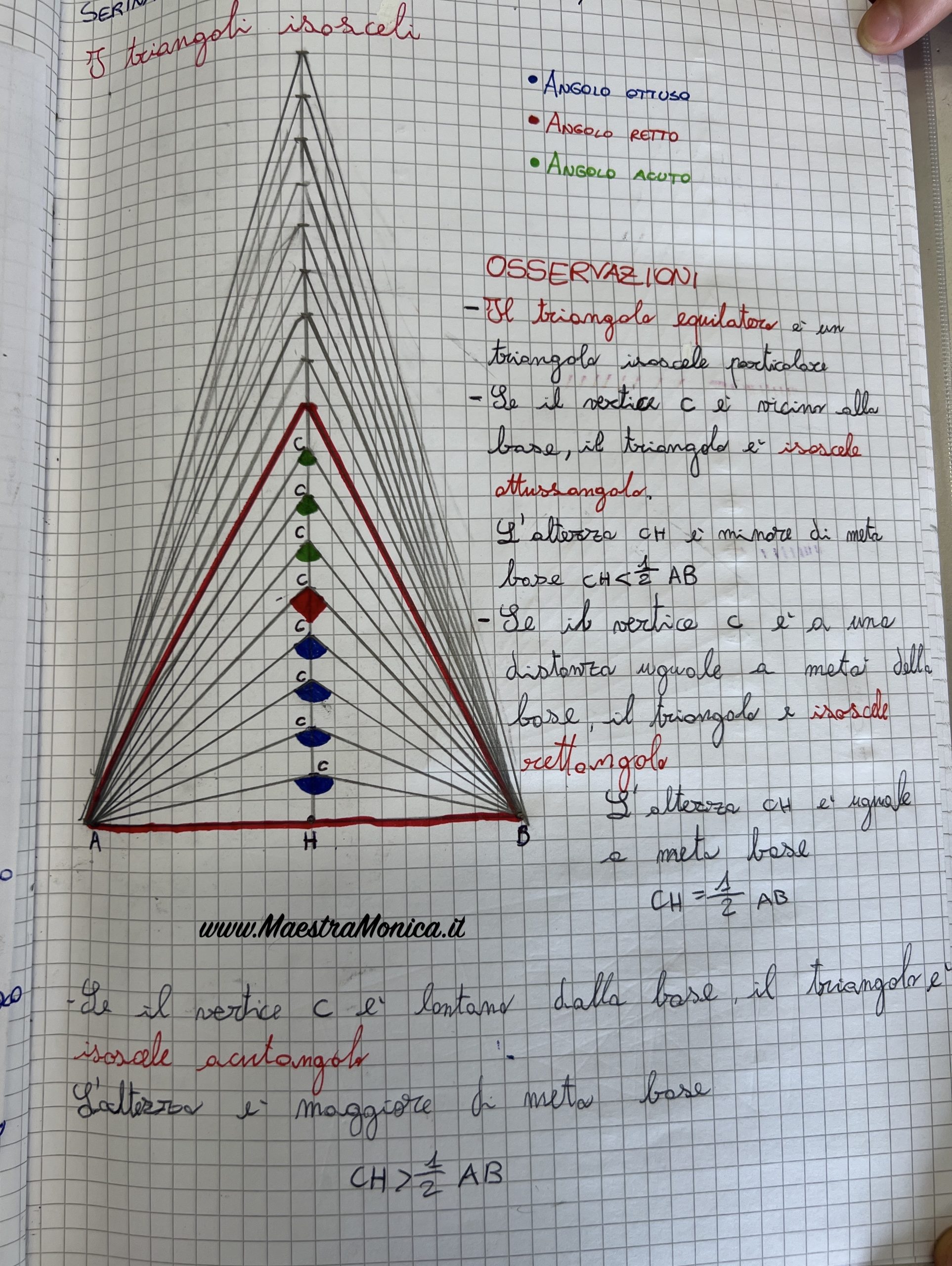
Gli alunni tracciano la BASE AB lunga 10 cm; trovano il PUNTO MEDIO H, cioè il punto che divide a metà la base (5 cm) dove vanno a disegnare l’ALTEZZA relativa alla base, cioè il segmento perpendicolare alla base. Sull’altezza riportano il VERTICE C nelle diverse posizioni.

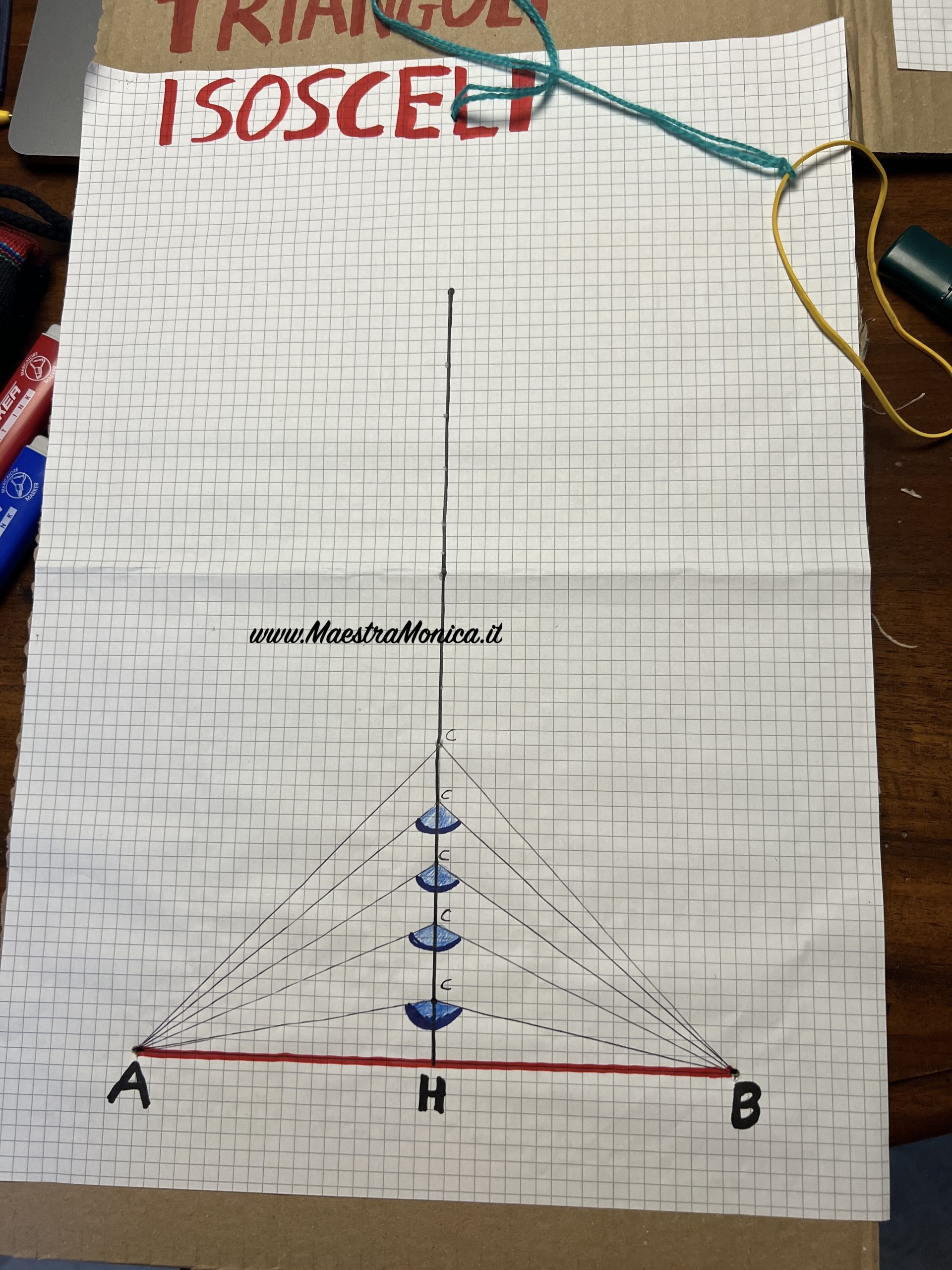

Utilizzando un “campione di angolo retto” i bambini individuano gli angoli ottusi, retti ed acuti e quindi classificano i triangoli rispetto agli angoli.
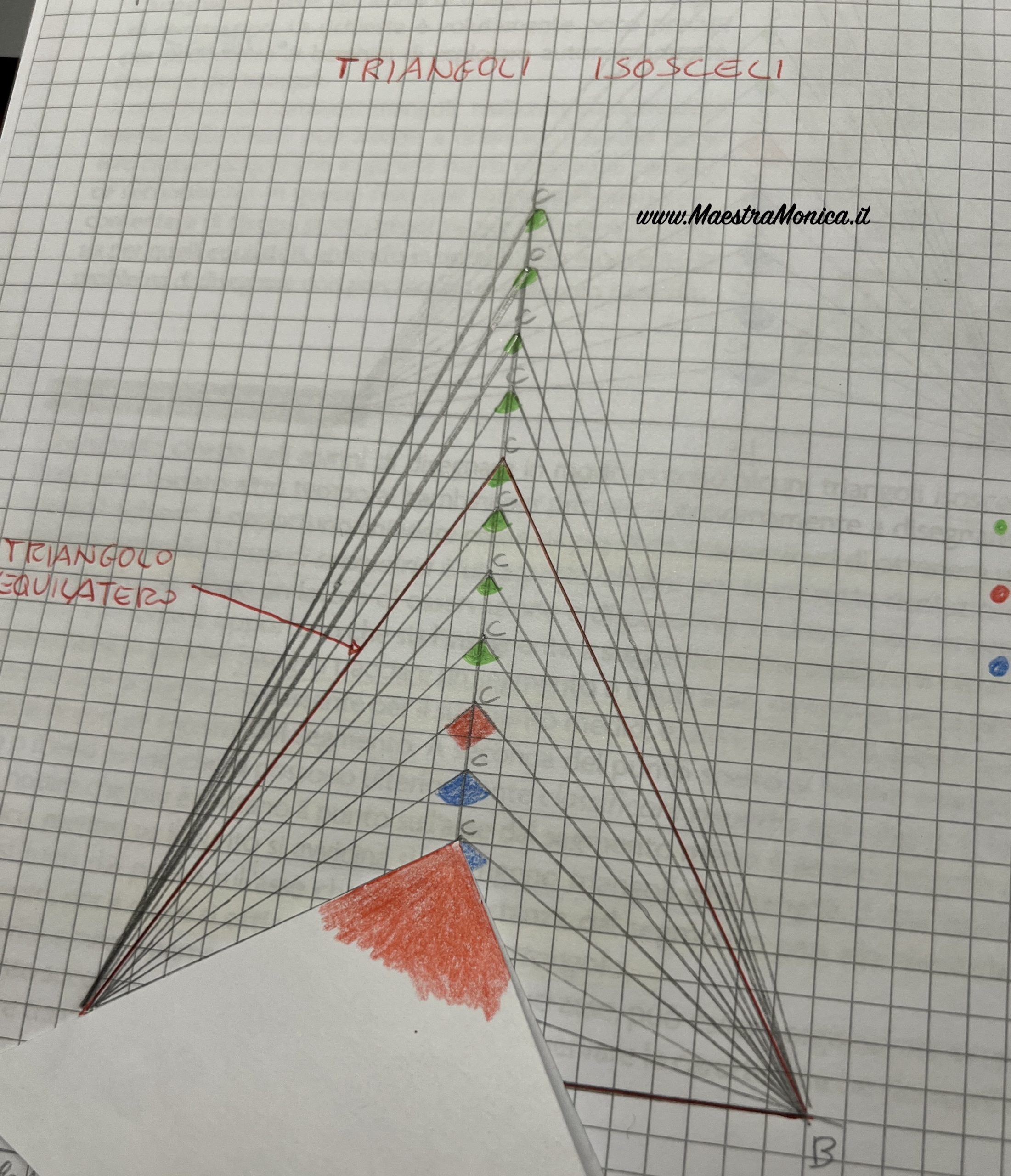
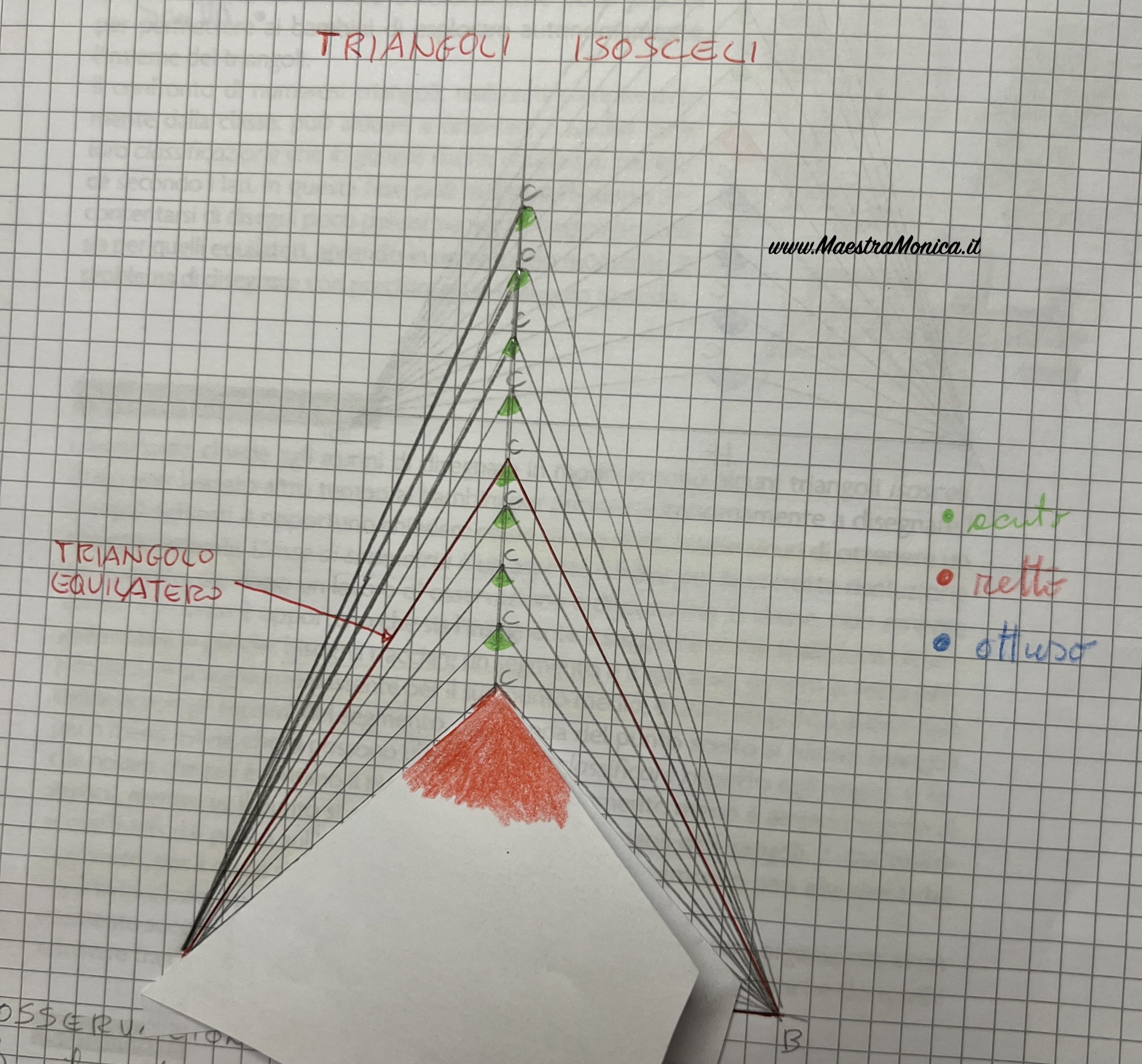
Si osserva la relazione tra altezza e base.
Se il vertice C è vicino alla base, l’angolo al vertice è più ampio dell’angolo retto e quindi il triangolo è isoscele ottusangolo. L’altezza CH è minore della metà della base.
CH < metà base
CH< 5 cm
Se il vertice C è a una distanza uguale alla metà della base, l’angolo al vertice è ampio come l’angolo retto e quindi il triangolo è isoscele rettangolo. L’altezza CH è uguale alla metà della base
CH = metà base
CH = 5 cm
Se il vertice C è lontano dalla base, l’angolo al vertice è più meno ampio dell’angolo retto e quindi il triangolo è isoscele acutangolo. L’altezza CH è maggiore della metà della base.
CH > metà base
CH > 5 cm
Continuando le nostre osservazioni scopriamo che tra i triangoli isosceli troviamo un caso particolare: il triangolo equilatero appartiene a questo gruppo!
IL TRIANGOLO EQUILATERO E’ UN TRIANGOLO ISOSCELE PARTICOLARE IN QUANTO HA ALMENO DUE LATI UGUALI.



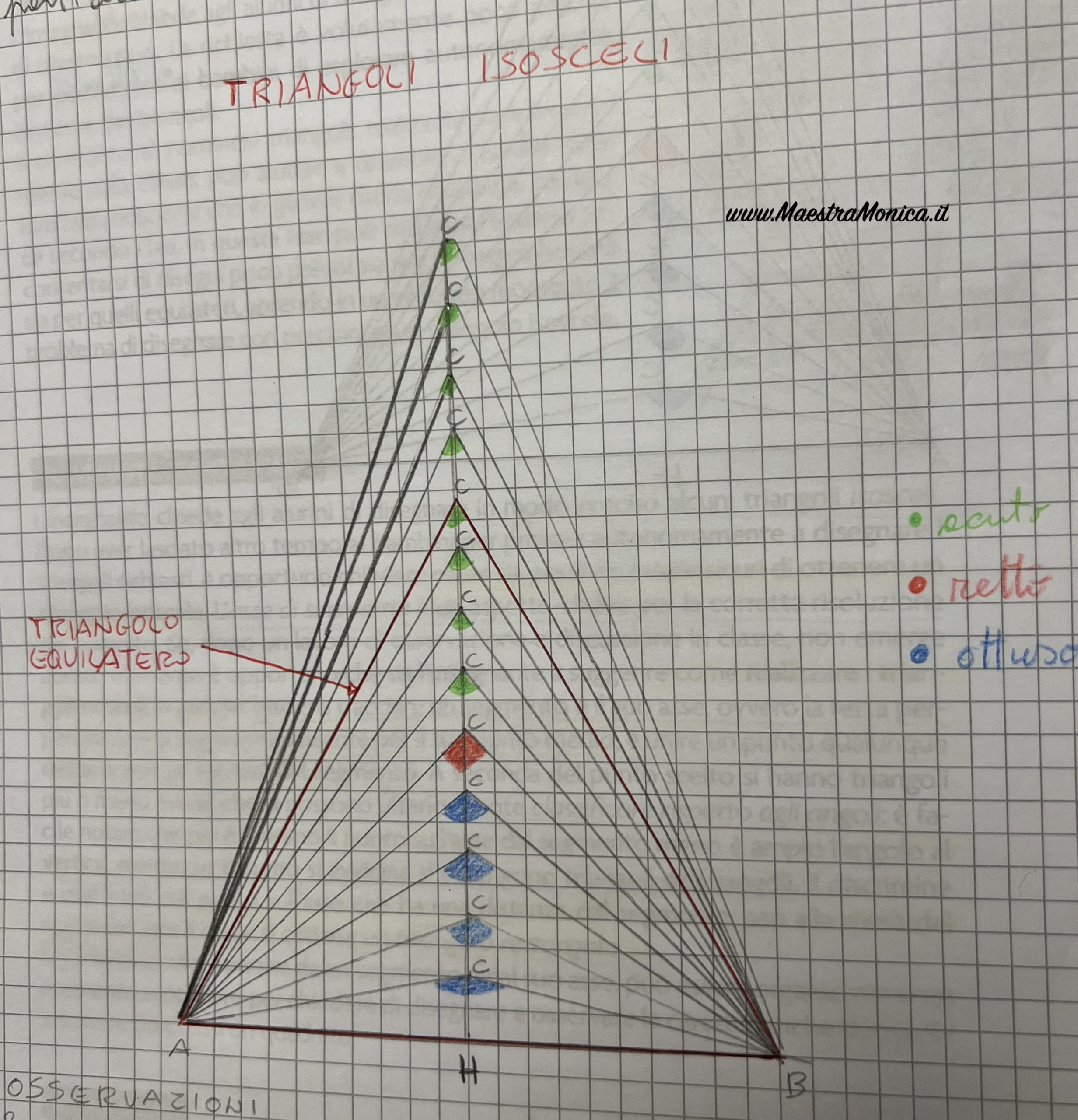
Questo lavoro di osservazione e discussione in classe è verbalizzato sul quaderno.

Dopo questa attività disegniamo i nostri triangoli e facciamo una tabella riassuntiva su tutti i possibili triangoli: 7 in tutto.
L’attività permette agli alunni di disegnare in modo preciso i triangoli isosceli: bisogna tracciare un segmento e il suo asse, ovvero la retta perpendicolare al segmento passante per il suo punto medio e unire un punto qualunque dell’asse con gli estremi del segmento.
