Il riconoscimento della congruenza di due figure può avvenire attraverso la sovrapposizione di una di esse all’altra per mezzo di un movimento rigido, una trasformazione geometrica o isometria. Per prendere confidenza con questa operazione, si propongono attività in cui le figure vengono fisicamente mosse. Come fatto per la traslazione, in cui la figura si sposta lungo una linea retta e la rotazione in cui lo spostamento avviene attorno ad un punto fisso a questo punto si opera con la simmetria, la trasformazione geometrica per cui la figura è ribaltata attorno ad una asse. Il nostro modello con cui i bambini ormai hanno preso confidenza è la girandola costruita con gli origami.
I bambini incollano su un foglio la figura in una posizione a scelta.



Sono sollecitati a riprodurre la girandola su un foglio da lucido che li motiva ad eseguire un disegno non approssimativo ed a ricercare la precisione.

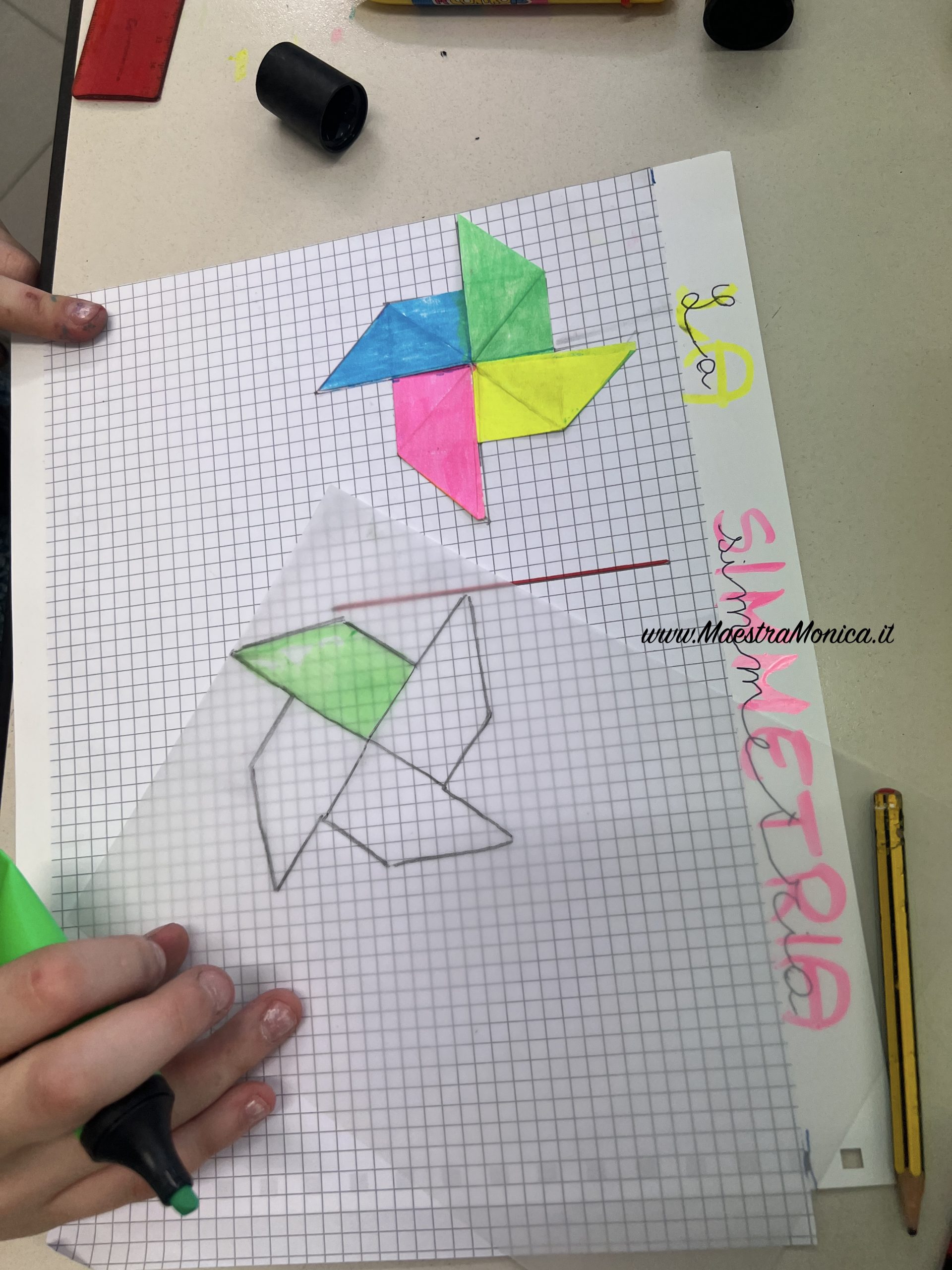

Il foglio da lucido fissato lungo l’asse di simmetria è ribaltato ed i bambini riportano la figura in posizione simmetrica.
Con la punta della matita appuntita i bambini determinano una serie di punti simmetrici con lo scopo di scoprire la relazione che lega i punti corrispondenti.


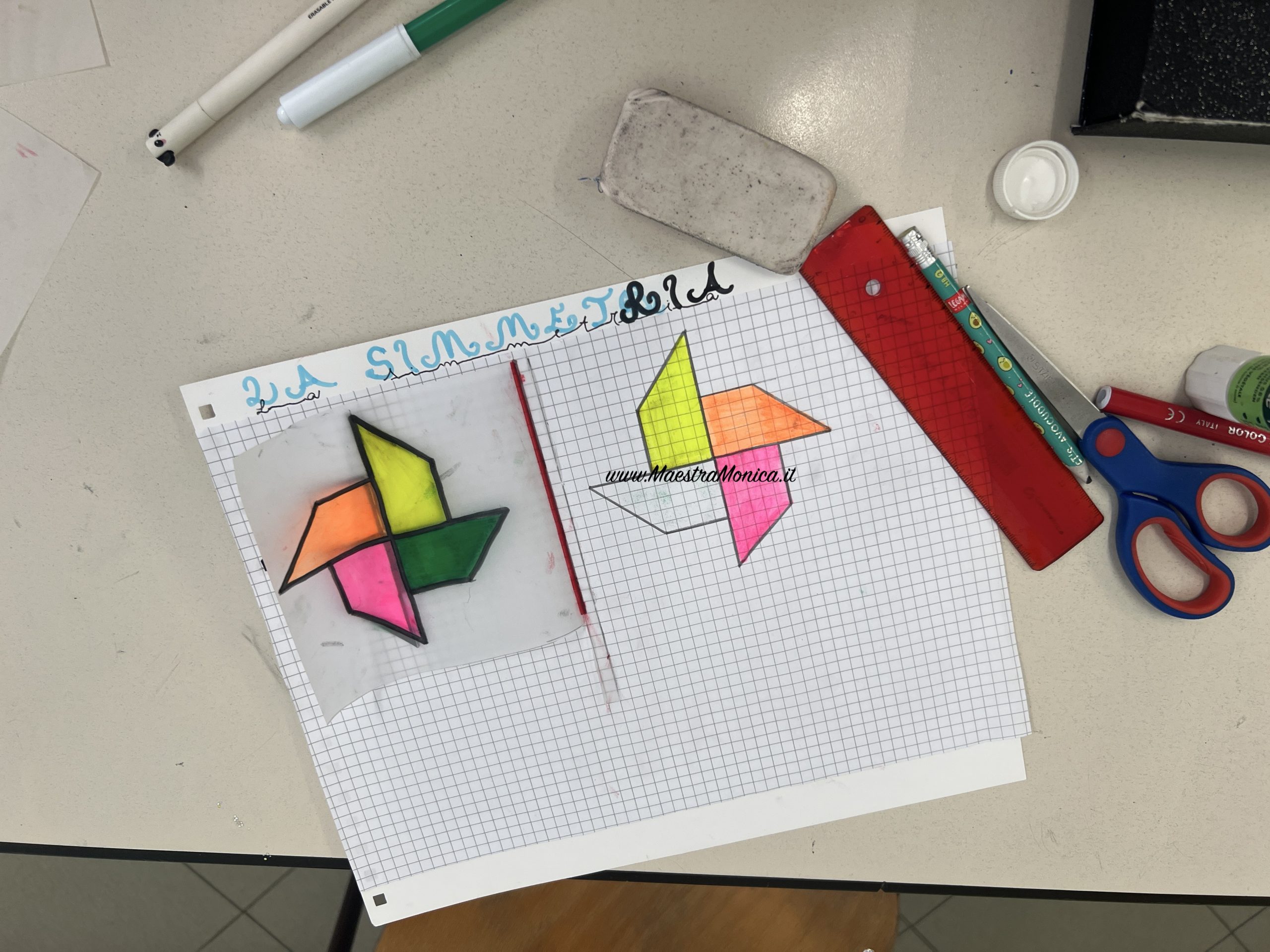

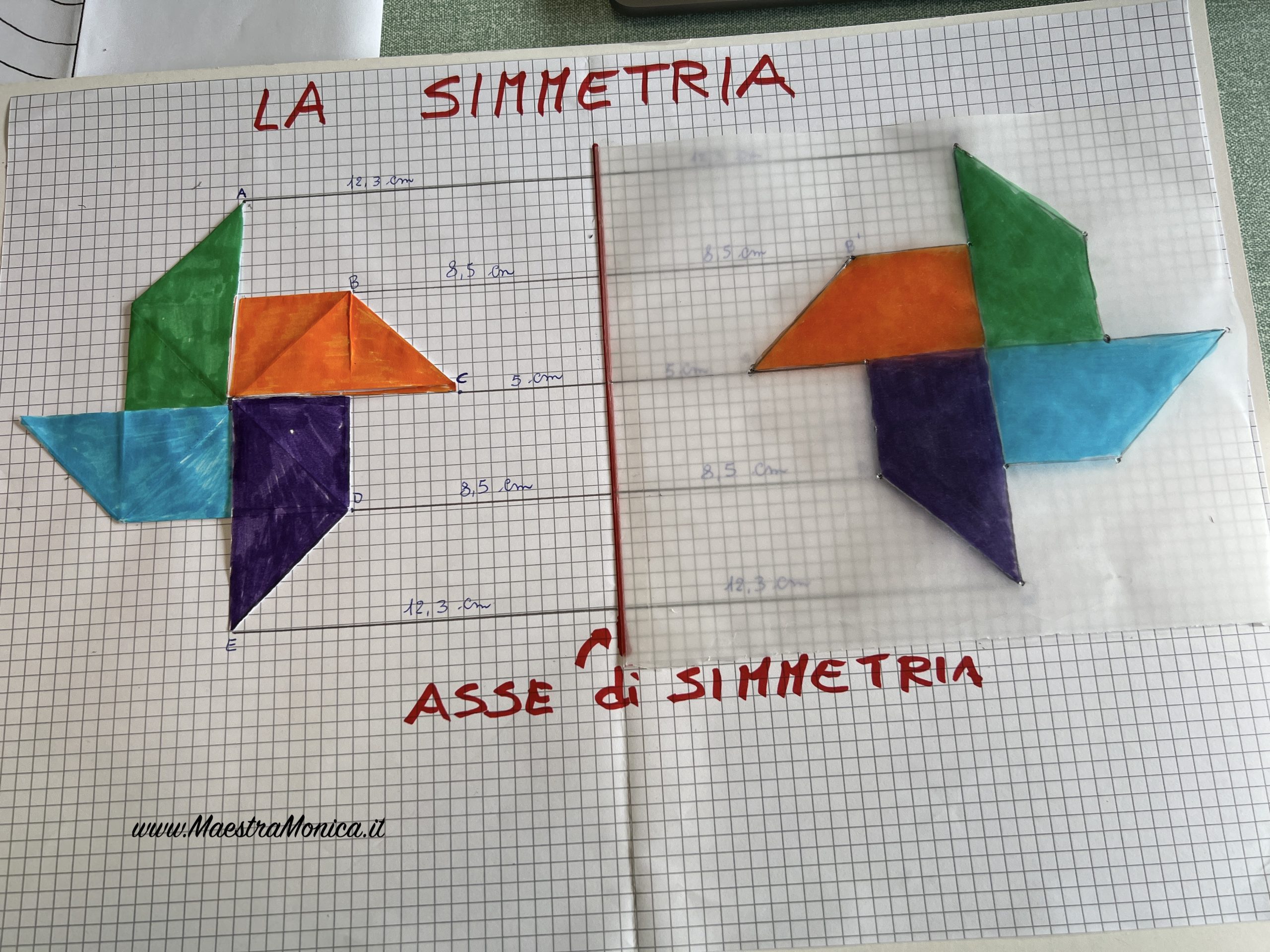
Per concludere si tracciano i segmenti che uniscono le coppie di punti simmetrici. Dalla loro osservazione si scopre la relazione implicata che può essere utilizzata come strumento per costruire figure simmetriche.
I punti simmetrici:
- sono equidistanti dall’asse di simmetria
I segmenti:
- sono paralleli tra loro
- sono perpendicolari all’asse di simmetria.

Altre proposte di trasformazioni geometriche
https://maestramonica.it/simmetria-specularita-e-ribaltamento-arte-e-geometria/
https://maestramonica.it/la-rotazione-angolo-di-rotazione-matematica-classe-5/
Altre accattivanti attività
https://playandlearnitalia.com/la-simmetria-con-gli-specchi-e-i-mandala/
