Stamattina i miei alunni mi anticipano e mi rammentano che oggi è la GIORNATA DEI CALZINI SPAIATI.
La Giornata dei Calzini Spaiati si celebra il primo venerdì del mese di febbraio per ricordare che tutti siamo diversi ma unici nella nostra bellezza.
Alcuni bambini indossano calzini spaiati.
Nei giorni precedenti, sono andata alla ricerca di un’attività di matematica da collegare alla giornata dei calzini spaiati. Perchè non proporre giochi di combinatoria e di possibilità, poco sviluppati in matematica, ma che il mondo scientifico supporta, suggerisce e pretende?
Di che si tratta? Si tratta di tutte quelle attività che servono a conteggiare i possibili accostamenti, le possibili disposizioni, le possibili combinazioni.
Qui riporto un articolo di Bruno d’Amore e Martha Isabel Fandiño Pinilla Probabilità, statistica, combinatoria: l’altra metà del cielo.
Ho cercato in rete e nei libri, anche di testo, che ho a disposizione, ma non trovo nulla che risponda alle mie aspettative.
Allora cerco tra la banca dei problemi del Rally matematico transalpino. Trovo i problemi “le bandierine” e “colorazione” e penso che possono benissimo essere adattati ai calzini.
Così preparo il lavoro che realizzo la mattina in classe e che qui riporto.
L’attività è stata aperta facendo insieme ai bambini una piacevole riflessione sul significato della Giornata dei Calzini Spaiati, di come ognuno di noi sia unico e diverso dagli altri.

I bambini…ma maestra è semplice…ogni striscia è di un solo colore…ogni calzino ha i tre colori…due strisce che si toccano non hanno lo stesso colore.
Allora…in ogni calzino due strisce hanno lo stesso colore o la striscia 1 e 3 oppure la 2 e 4 o ancora la 1 e 4.
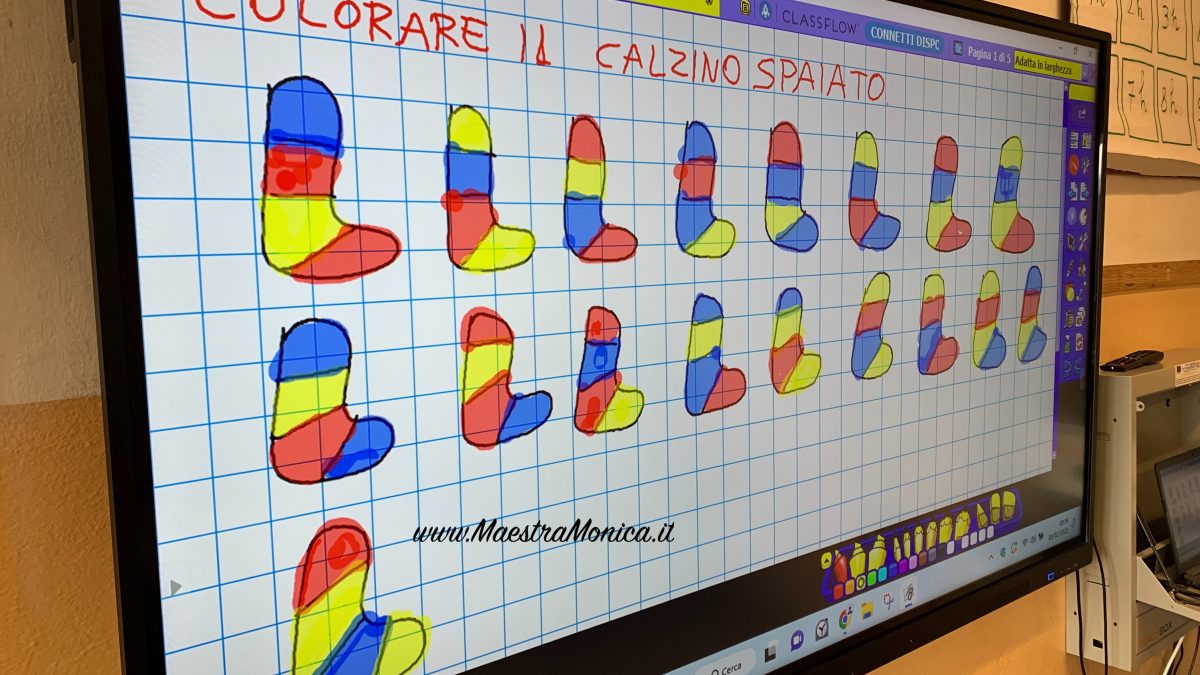
In questo primo momento i calzini sono disegnati in modo non ordinato.
Un bambino alla volta colora il suo calzino alla LIM fino all’esaurimento delle combinazioni.
Al 19° bambini, gli alunni constatano che non ci sono più possibilità di colorare le quattro strisce in un modo diverso e che i 21 bambini non potranno avere dei calzini tutti diversi. Solo 18 hanno calzini diversi, mentre 3 li hanno uguali.
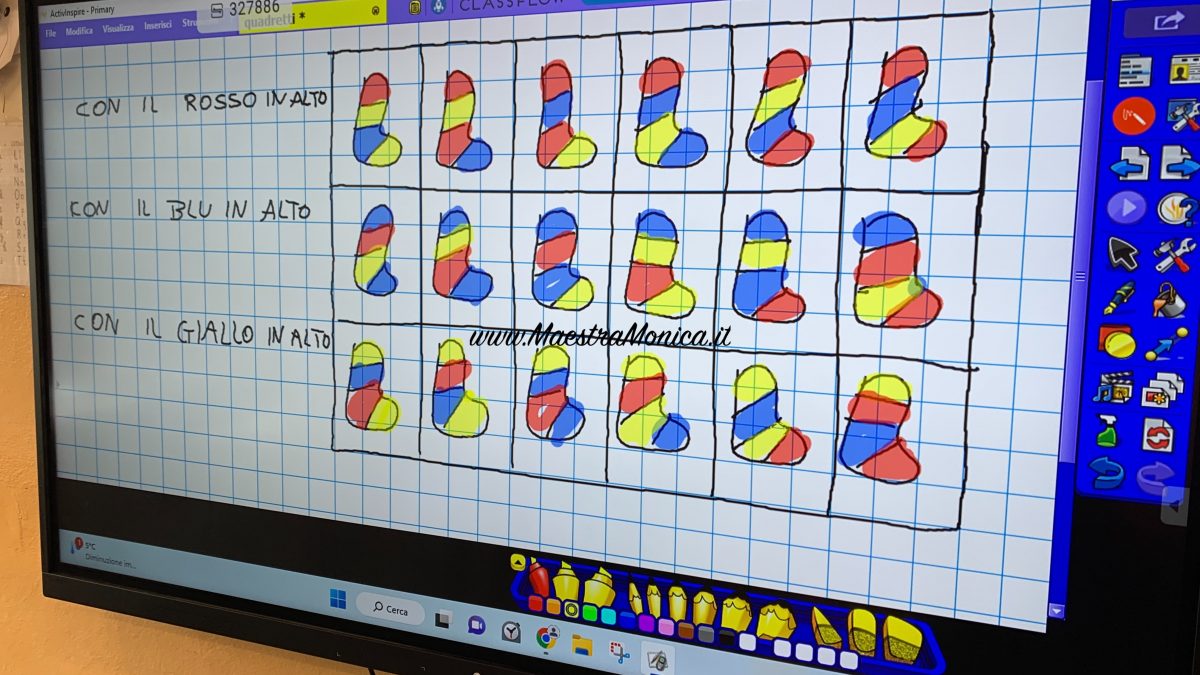
Successivamente si procede ad organizzare le combinazioni in modo sistematico inserendo i calzini in una tabella: CON IL ROSSO IN ALTO, CON IL GIALLO IN ALTO, CON IL BLU IN ALTO.
Ancora una volta i bambini, uno alla volta, colorano nuovamente i calzini in tabella alla LIM secondo le possibilità offerte.

Infine si utilizza anche un diagramma ad albero per organizzare le possibilità.
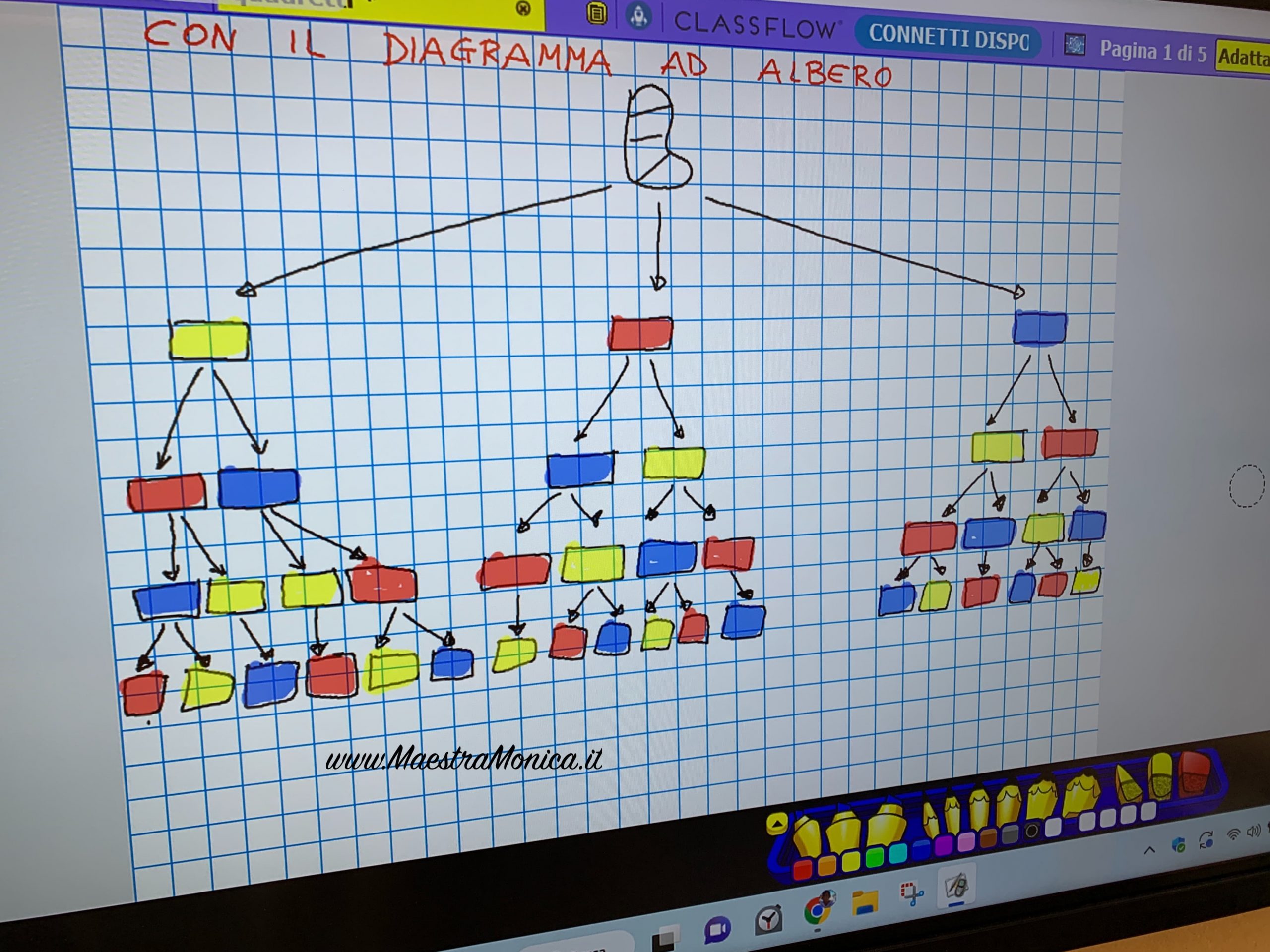

Tre possibilità per la prima riga: R ; G; B ; due scelte per ognuna delle tre per la seconda riga: RG; RB; GR; … quindi 6 possibilità; per la terza riga ci sono di nuovo due scelte per ognuna delle possibilità precedenti e si arriva così a 12 combinazioni RGB; RGR; RBR; RBG; GRG; ….
Tra le combinazioni precedenti, sei hanno due colori, RGR; RBR; GRG;… le altre sei hanno tre colori ; RGB; RBG; GRB; … le prime devono obbligatoriamente essere completate con il terzo colore, le seconde offrono ancora, ognuna, due possibilità per la quarta riga, ciò che conduce alle 18 (6 + 2 × 6) combinazioni possibili: